Conocimiento Personal
Aun sigo viendo este tema un poco complicado, pero ya con las estudiadas entre semana se me ha ido facilitando un poco más, aprendí que (e^x) nunca va a cambiar al derivar si no que siempre será igual, también entendí que normalmente en estas derivadas se usan casi todas las reglas, puede tener de producto, cadena, etc.
Conocimiento Consultado
Derivada de la función exponencial
La derivada de la función exponencial es igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente.
Derivada de la función exponencial de base e
La derivada de la función exponencial de base e es igual a la misma función por la derivada del exponente.
Derivada de e a la x
Para el caso especial
Tenemos que
Siguiendo la fórmula anterior
Se concluye que
Y así, decimos que la derivada de 
es
Derivada del logaritmo natural
Si la base del logaritmo es el número de Euler, 
, entonces se logaritmo se conoce como logaritmo natural (o logaritmo neperiano). En este caso lo denotamos
Si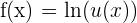 
, entonces la derivada del logaritmo natural es
donde ya estamos tomando en cuenta la regla de la cadena.
En particular, la derivada de 
es
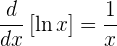
Fuentes de Información
https://www.superprof.es/apuntes/escolar/matematicas/calculo/derivadas/derivada-de-la-funcion-exponencial.html
https://www.superprof.es/apuntes/escolar/matematicas/calculo/derivadas/derivadas-logaritmicas.html
https://www.youtube.com/watch?app=desktop&v=wl1joYQQ3CI&t=65s
https://www.youtube.com/watch?v=bEmCMdwXy5o
https://www.youtube.com/watch?v=krZ92qtMwkY
Comentarios
Publicar un comentario