INTEGRALES DEFINIDAS

el

  Conocimiento Personal

Me gusto un poco más este tema que el anterior, ya que le entendí un poco más, además que nos ayudó un poco con la calculadora para saber cómo se usa y eso fue un plus, ya que, si es importante saber usarla para que se le dificulte a uno menos hacer los ejercicios, tareas o exámenes

La integral definida es el área limitada por una función en un sistema de coordenadas cartesianas.

La integral definida se representa con la expresión:


Donde a y b son límites de integración inferior y superior.

Conocimiento Consultado

Desde su origen, la noción de integral ha respondido a la necesidad de mejorar los métodos de medición de áreas subtendidas bajo líneas y superficies curvas. La técnica de integración se desarrolló sobre todo a partir del siglo XVII, paralelamente a los avances que tuvieron lugar en las teorías sobre derivadas y en el cálculo diferencial

Concepto de Integral definida
La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.


Propiedades de la Integral Definida

La integral definida cumple las siguientes propiedades:

  • Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
  • Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
  • La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
  • La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
  • Al permutar los límites de una integral, ésta cambia de signo.
  • Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):


Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:


Teorema fundamental del cálculo Integral 

La relación entre derivada e integral definida queda establecida definitivamente por medio del denominado teorema fundamental del cálculo integral, que establece que, dada una función f (x), su función integral asociada F (x) cumple necesariamente que:


A partir del teorema fundamental del cálculo integral es posible definir un método para calcular la integral definida de una función f (x) en un intervalo [a, b], denominado regla de Barrow:

  • Se busca primero una función F (x) que verifique que F¿ (x) = f (x).
  • Se calcula el valor de esta función en los extremos del intervalo: F (a) y F (b).
  • El valor de la integral definida entre estos dos puntos vendrá entonces dado por:
Ejemplo de aplicación
En este ejemplo implementaremos las propiedades anteriores en una aplicación de la integral en crecimiento poblacional, para una mejor visualización.

Una población crece con una tasa de 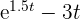 individuos por año (donde  es el número de años).  En el primer año la población es de 1500 personas.

¿Cuánto creció la población entre en primer y tercer año?, ¿Cuál es la población en el tercer año?

1  Dado que nos pide el crecimiento de la población entre 1 y 3, es decir, el área bajo la curva de la tasa de crecimiento entre 1 y 3, lo expresaremos como sigue:

Nota: los pasos siguientes son para ilustrar el uso de las propiedades, algunos de ellos pueden ser omitidos.

2 Al hacer los cálculos,  notemos que podemos usar la propiedad 4 y separamos en una suma.

3  También podemos utilizar la propiedad 5 y sacamos el la constante -3 que multiplica a t.

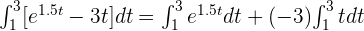
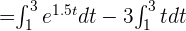
4 Dado que 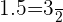 sustituimos y hacemos los cálculos que correspondientes para hallar la respuesta a la primera pregunta:

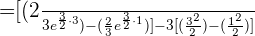
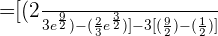
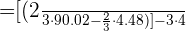
Así el crecimiento entre el primer y tercer año fue de 33 individuos aproximadamente.

6  Para la segunda pregunta seguimos es siguiente razonamiento:

  • En el año 1 la población era de 1000 individuos.
  • El crecimiento entre el año 1 y 3 fue de 33 individuos aproximadamente.
  • Así la población al en el año 3 es de 1033 individuos aproximadamente.










Fuentes de Información

https://www.hiru.eus/es/matematicas/la-integral-definida

https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/integrales-definidas.html

https://www.youtube.com/watch?v=_j3Mgxtooyk

https://www.youtube.com/watch?v=jBoJzwiXFZw&list=PLeySRPnY35dFOQ6o4yXOgjIpZ0IX3sVg1&index=4


Comentarios

Publicar un comentario