CÁLCULO DE ÁREAS ENTRE 2 GRÁFICOS

 Conocimiento Personal

Este tema se me hizo muy interesante, aunque la verdad se me está haciendo algo muy complicado, con solo la clase vi que si era algo complejo y ahora que he visto videos se me sigue haciendo complicado.

Esto es algo de lo que aprendí una función f(x) integrable en los intervalos [a,b], en el área de la región limitada por la función, el eje "0x" y las rectas x=a, x=b.

Conocimiento Consultado

El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo.

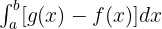
Ejemplo Resuelto del Área entre 2 Funciones 

Calcular el área limitada por la curva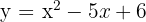   

y la recta   .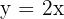

En primer lugar, hallamos los puntos de corte de las dos funciones para conocer los límites de integración.

Esto lo haremos al resolver la ecuación

, es decir, igualando las funciones.

De  a , la recta queda por encima de la parábola. Entonces el área va a estar dada por:

El Área entre 2 Curvas 

En esta sección estudiaremos como calcular el área entre dos curvas. 

El problema es el siguiente: Dadas dos funciones f y g, encontrar el área contenida entre sus gráficas en el intervalo [a,b].

Para ilustrar el problema y el procedimiento, observa el siguiente ejemplo:

1. Evaluamos f(x*) yg(x*) y formamos rectángulos de base (b-a)/n y de altura f(x*)-g(x*) (si f(x*)>g(x*)).

2. El área de dicho rectángulo es (f(x*)-g(x*)) ((b-a) /n). Al sumar las áreas de los rectángulos obtenemos una aproximación al valor del área entre las curvas.

3. Tomando el límite cuando n-Infinito obtendremos el valor exacto del área buscada.

4. Por definición, el límite de la sumatoria de Riemann es la integral definida de f(x)-g(x) en [a,b].

5. Si g(x)>f(x) en alguna parte del intervalo, entonces la altura de los rectángulos es g(x*)-f(x*).

Fuentes de Información

https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/area-comprendida-entre-dos-funciones.html

https://www.uacj.mx/CGTI/CDTE/JPM/Documents/IIT/sterraza/mate2016/areas/area_dos.html

https://www.youtube.com/watch?v=5ZrfmQEVMjk&list=PLeySRPnY35dEHnMLZGaNEXgHzJ2-TPLWw&index=101

https://www.youtube.com/watch?v=s1BMqFdtZfM&list=PLeySRPnY35dEHnMLZGaNEXgHzJ2-TPLWw&index=102