Conocimiento Personal
Se me hizo un tema muy interesante donde puedes usar la fórmula de la mentada VACA:
esta es usada para la integración por partes y aplica cuando 2 funciones están multiplicando o dividiendo.
Donde u: Tiene que ser una f(x) fácil de derivar
dv: Tiene que ser una f(x) fácil de integrar
Se usan varios tipos de funciones que también son llamadas como ILATE.
Fue un tema entendible, aunque si lo vi un poco complicado, pero con los videos y la práctica poco a poco será un poco más sencillo.
Conocimiento Consultado
La Integración por Partes es un método especial de integración que suele ser útil cuando se multiplican dos funciones, pero también es útil de otras formas.
Pronto verás muchos ejemplos, pero primero veamos la regla:
∫u·dv dx = u·v −∫v·du dx
- u es la función u(x)
- v es la función v(x)
- du es la derivada de la función u(x)
- dv es la derivada de la función v(x)
Como diagrama:
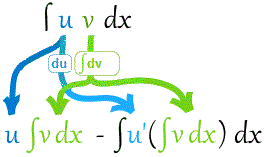
Vayamos directamente a un ejemplo y hablemos del diagrama después:
Ejemplo: Hallar la integral ∫x cos(x) dx
OK, tenemos x multiplicando a cos(x), así que usar integración por partes es una buena elección.
Primero elige quién es u y quién es dv:
- u = x
- dv = cos(x)
Así que ahora que tenemos ∫u dv dx podemos continuar:
Deriva u: du = x' = 1
Integra dv: v = ∫dv dx = ∫cos(x) dx = sin(x)
Ahora lo podemos poner junto:
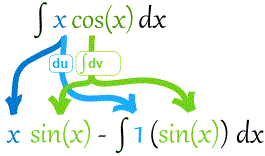
Simplifica y resuelve:
Lo que hicimos fue seguir estos pasos:
- Elegir u y dv
- Derivar u: du
- Integrar dv: ∫dv dx
- Poner u, v y du en: uv −∫vdu dx
- Simplificar y resolver
En español, hay una manera mnemotécnica para recordar la integración por partes. Sabiendo que, u y v son funciones de x, no escribiremos el dx, así:
∫u·dv = u·v −∫v·du
Un Día Vi Una Vaca sin cola Vestida De Uniforme
o también
un día vi una vaca sin cola vestida de unicornio
En realidad, hay muchas otras frases que ayudan a recordar la integración por partes. La clave en este caso sería recordar, además de la frase, dónde va el signo igual y que "sin cola" significa "menos la integral de".
Por cierto, esta frase mnemotécnica es la razón por la cual algunos se refieren cariñosamente a la Integración por Partes como el Teorema de la Vaquita.
Probemos alguno ejemplo más:
La moraleja de la historia: ¡Elige u y dv con cuidado!
Elige una u que se vuelva más simple cuando la derives y una dv que no se vuelva más complicada cuando la integres.
Una regla que puedes memorizar es ILATE. Elige u en función de cual de estas viene primero:
- I: Inversas trigonométricas, tales como sin-1(x), cos-1(x), tan-1(x)
- L: Logarítmicas, tales como ln(x), log(x)
- A: Algebraicas, tales como x2, x3
- T: Trigonométricas, tales como sin(x), cos(x), tan (x)
- E: Exponenciales, tales como ex, 3x

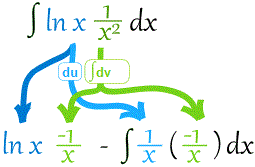
Comentarios
Publicar un comentario